12.6 ROC Curves

  • ROC curves show the balance between sensitivity and specificity.
  • We’ll use the [ROCR] package. It only takes 3 commands:
    • calculate prediction() using the model
    • calculate the model performance() on both true positive rate and true negative rate for a whole range of cutoff values.
    • plot the curve.
      • The colorize option colors the curve according to the probability cutoff point.
pr <- prediction(phat.depr, dep_sex_model$y)
perf <- performance(pr, measure="tpr", x.measure="fpr")
plot(perf, colorize=TRUE, lwd=3, print.cutoffs.at=c(seq(0,1,by=0.1)))
abline(a=0, b=1, lty=2)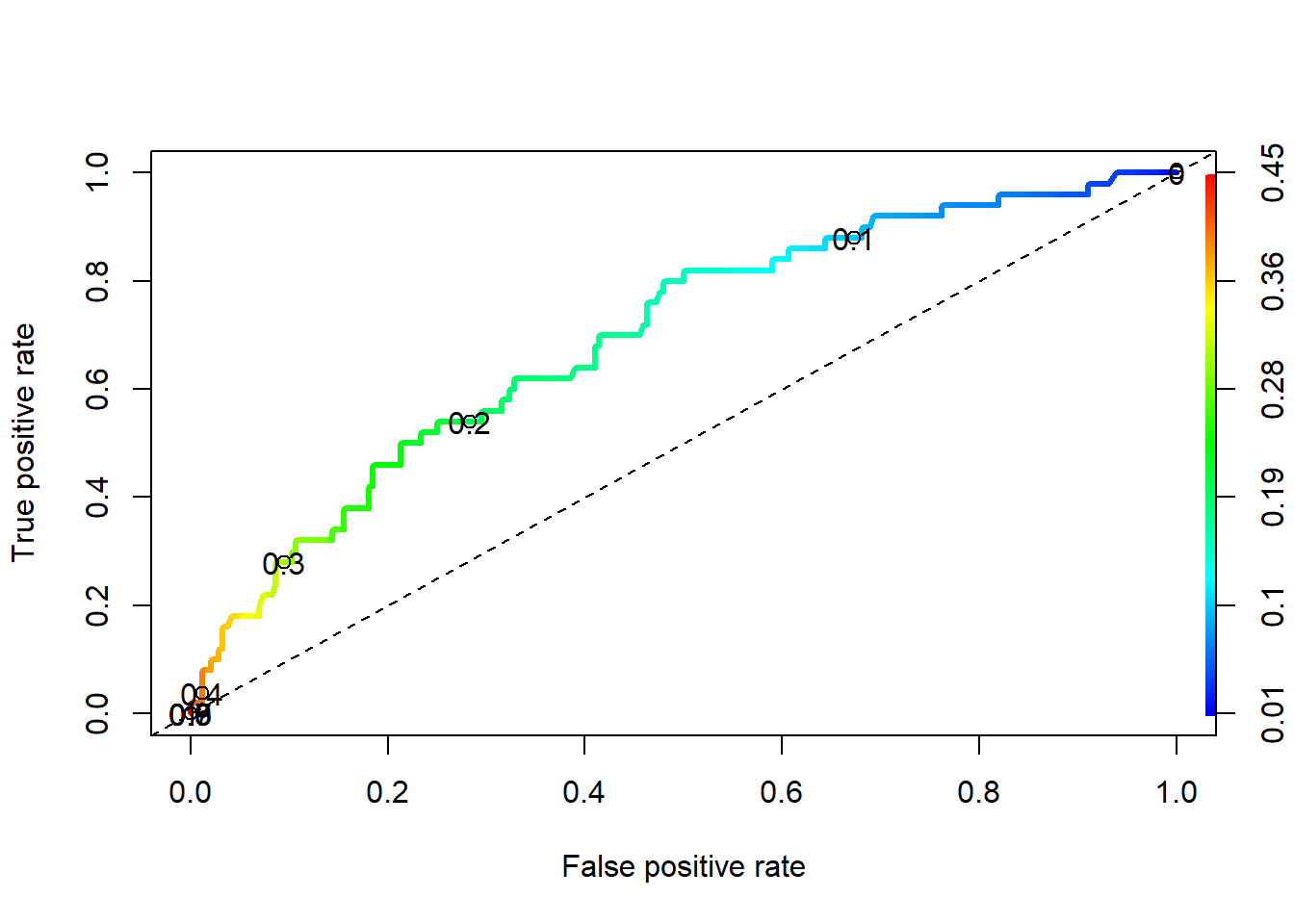

We can also use the performance() function to evaluate the \(f1\) measure

perf.f1 <- performance(pr,measure="f")
perf.acc <- performance(pr,measure="acc")

par(mfrow=c(1,2))
plot(perf.f1)
plot(perf.acc)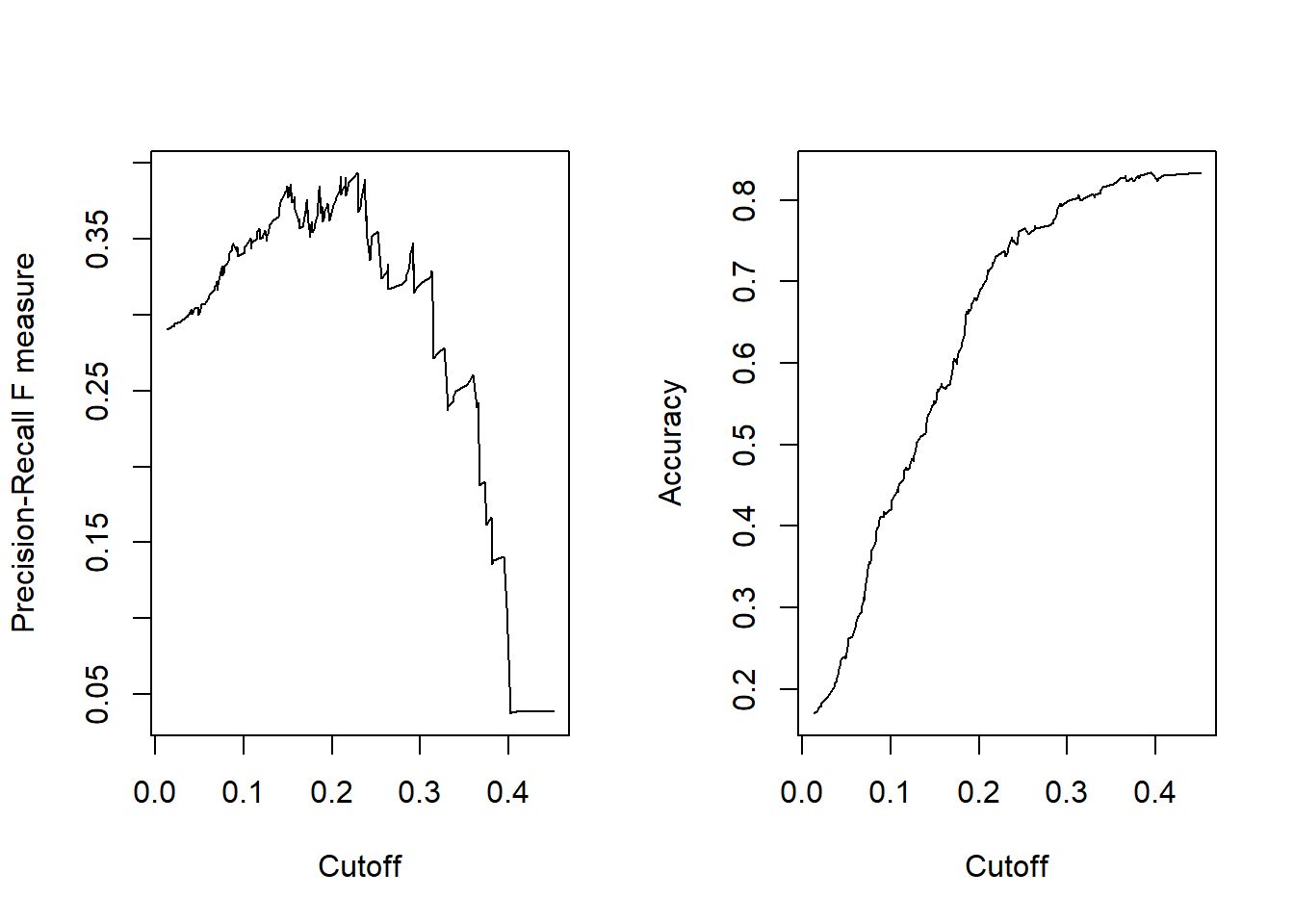

We can dig into the perf.f1 object to get the maximum \(f1\) value (y.value), then find the row where that value occurs, and link it to the corresponding cutoff value of x.

(max.f1 <- max(perf.f1@y.values[[1]], na.rm=TRUE))
## [1] 0.3937008
(row.with.max <- which(perf.f1@y.values[[1]]==max.f1))
## [1] 68
(cutoff.value <- perf.f1@x.values[[1]][row.with.max])
##       257 
## 0.2282816

A cutoff value of 0.228 provides the most optimal \(f1\) score.

ROC curves:

auc <- performance(pr, measure='auc')
auc@y.values
## [[1]]
## [1] 0.695041