16.1 Example School Data

The data used in this first example comes from a publicly available data set called the National Education Longitudinal Study of 1988 (yes it’s a bit old data, but sufficient for our purposes here). In this data set math scores are recorded for 519 students from 23 schools.

List a few characteristics that you think are associated with math performance, and at what level they are measured.

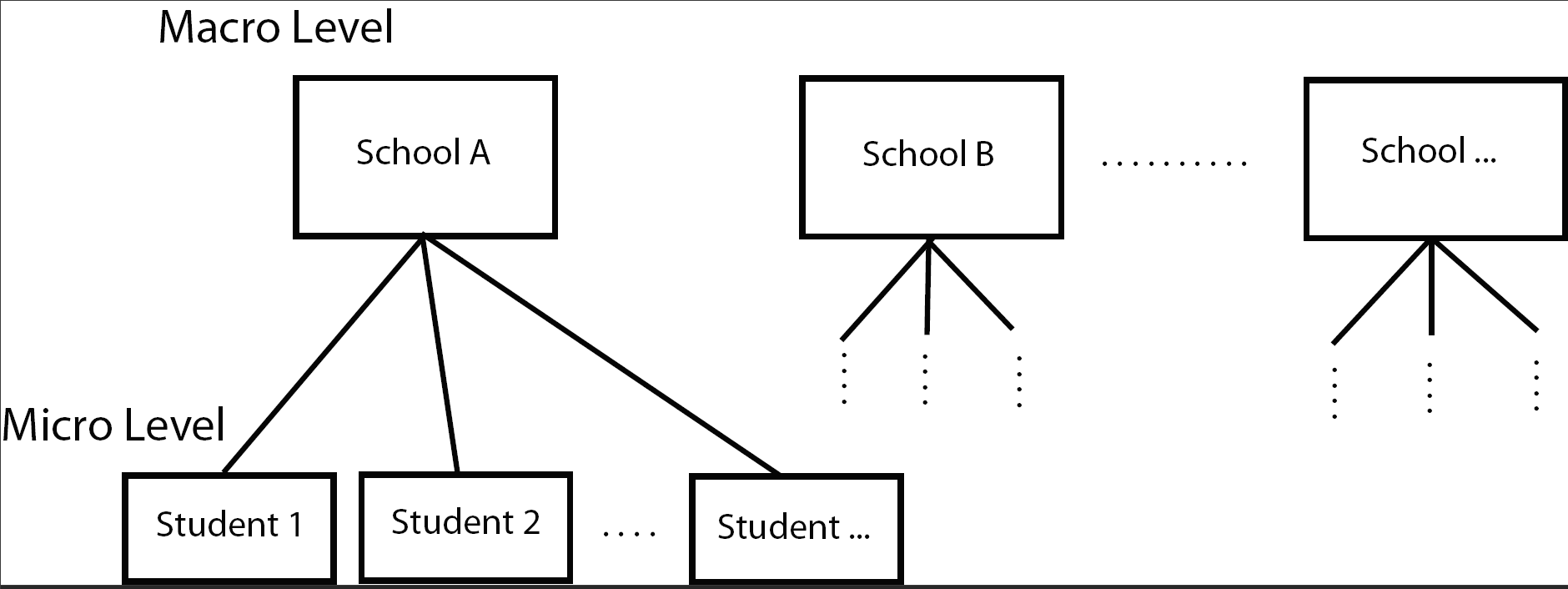
The School23 data set contains the following variables:

• School (macro) level variables
  • School type
  • class structure
  • school size
  • urbanity
  • geographic region
  • percent minority
  • student-teacher ratio
• Student (micro) level variables
  • Gender
  • Race
  • Time spent on math homework
  • SES
  • parental education
  • math score

Imagine a model of math score based on school type (\(X_{1}\) 1 for public, 0 for private) and SES (\(X_{2}\)).

\[ Y_{i} = \beta_{0} + \beta_{1}X_{1i} + \beta_{2}X_{2i} + \epsilon_{i}, \qquad i = 1, \ldots, n=519 \]

This model does not take into the account the hierarchical nature of the data in that students are nested within schools. School type is a macro level variable, SES is a micro level variable. We could consider adding indicator variables for each of the 23 schools to create a Fixed Effects model,

\[ Y_{i} = \beta_{0} + \beta_{1}(SchoolType)_{1i} + \beta_{2}(SES)_{2i} + \beta_{3}(School2)_{i} + \ldots + \beta_{24}(School23)_{i} + \epsilon_{i} \]

but we already are well aware of fitting models with that many parameters, and when some school only have a few students in them. So we need a different model.