8.1 Moderation

Moderation occurs when the relationship between two variables depends on a third variable.

  • The third variable is referred to as the moderating variable or simply the moderator.
  • The moderator affects the direction and/or strength of the relationship between the explanatory (\(x\)) and response (\(y\)) variable.
    • This tends to be an important
  • When testing a potential moderator, we are asking the question whether there is an association between two constructs, but separately for different subgroups within the sample.
    • This is also called a stratified model, or a subgroup analysis.

8.1.1 Motivating Example - Admissions at UC Berkeley

Sometimes moderating variables can result in what’s known as Simpson’s Paradox. This has had legal consequences in the past at UC Berkeley.

Below are the admissions figures for Fall 1973 at UC Berkeley.

Table of admissions rates at UC Berkeley in 1973
Applicants Admitted
Total 12,763 41%
Men 8,442 44%
Women 4,321 35%

Is there evidence of gender bias in college admissions? Do you think a difference of 35% vs 44% is too large to be by chance?

Department specific data

The table of admissions rates for the 6 largest departments show a different story.
All Men Women
Department Applicants Admitted Applicants Admitted Applicants Admitted
A 933 64% 825 62% 108 82%
B 585 63% 560 63% 25 68%
C 918 35% 325 37% 593 34%
D 792 34% 417 33% 375 35%
E 584 25% 191 28% 393 24%
F 714 6% 373 6% 341 7%
Total 4526 39% 2691 45% 1835 30%

After adjusting for features such as size and competitiveness of the department, the pooled data showed a “small but statistically significant bias in favor of women”

8.1.2 Motivating Example: Association of flower parts

Let’s explore the relationship between the length of the sepal in an iris flower, and the length (cm) of it’s petal.

overall <- ggplot(iris, aes(x=Sepal.Length, y=Petal.Length)) + 
                geom_point() + geom_smooth(se=FALSE) + 
                theme_bw()

by_spec <- ggplot(iris, aes(x=Sepal.Length, y=Petal.Length, col=Species)) + 
                  geom_point() + geom_smooth(se=FALSE) + 
                  theme_bw() + theme(legend.position="top")

gridExtra::grid.arrange(overall, by_spec , ncol=2)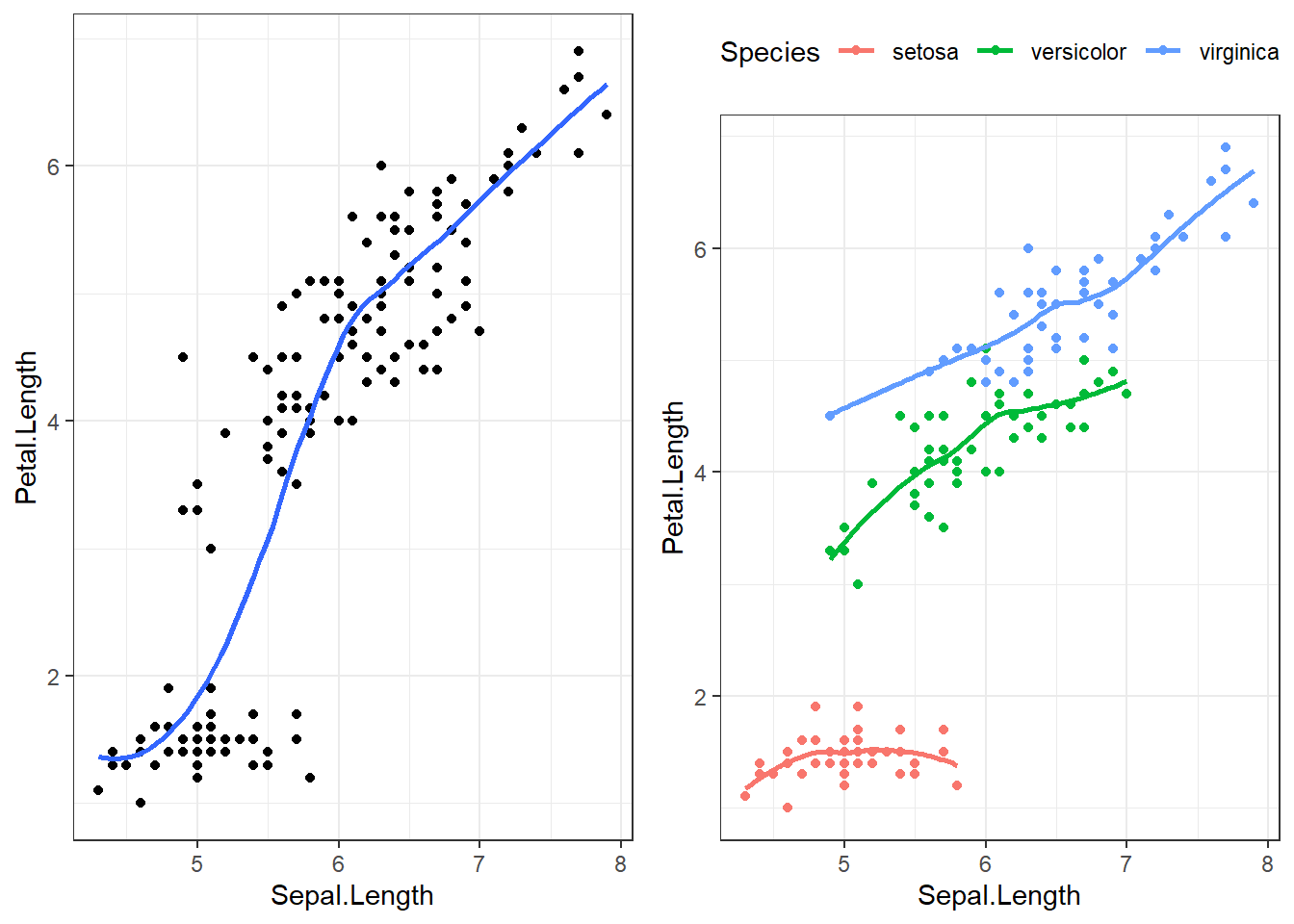

The points are clearly clustered by species, the slope of the lowess line between virginica and versicolor appear similar in strength, whereas the slope of the line for setosa is closer to zero. This would imply that petal length for Setosa may not be affected by the length of the sepal.