17.4 Fitting models in R

Complete Pooling

The complete pooling model is fit with the function lm, and is only modeled by 1 and no covariates. This is the simple mean model, and is equivelant to estimating the mean.

fit_completepool <- lm(log_radon ~ 1, data=radon)
fit_completepool
## 
## Call:
## lm(formula = log_radon ~ 1, data = radon)
## 
## Coefficients:
## (Intercept)  
##       1.265
mean(radon$log_radon)
## [1] 1.264779

No Pooling

The no pooling model is also fit with the function lm, but gives each county a unique intercept in the model.

fit_nopool <- lm(log_radon ~ -1 + county, data=radon)
fit_nopool.withint <- lm(log_radon ~ county, data=radon)
Dependent variable:
log_radon
(1) (2)
Constant 0.715* (0.383)
countyAITKIN 0.715* (0.383)
countyANOKA 0.891*** (0.106) 0.176 (0.398)
countyBECKER 1.090** (0.443) 0.375 (0.585)
Note: p<0.1; p<0.05; p<0.01
  • The first model (fit_nopool) is coded as lm(log_radon ~ -1 + county, data=radon), and so does not have the global intercept (that’s what the -1 does). Each \(\beta\) coefficient is the estimate of the mean log_radon for that county.
  • The second model (fit_nopool.withint) is coded as lm(log_radon ~ county, data=radon) and is what we are typically used to fitting.
    • Each estimate is the difference in log(radon) for that county compared to a reference county.
    • Because county is alphabetical, the reference group is AITKIN.
    • Aitkin’s mean level of log(radon) shows up as the intercept or Constant term.
  • For display purposes only, only the first 3 county estimates are being shown.

Partial Pooling

  • The partial pooling model is fit with the function lmer(), which is part of the lme4 package.
  • The extra notation around the input variable (1|county) dictates that each county should get its own unique intercept \(\alpha_{j[n]}\).
fit_partpool <- lmer(log_radon ~ (1 |county), data=radon)

The fixed effects portion of the model output of lmer is similar to output from lm, except no p-values are displayed. The fact that no p-values are displayed is a much discussed topic. The author of the library lme4, Douglas Bates, believes that there is no “obviously correct” solution to calculating p-values for models with randomly varying intercepts (or slopes); see here for a general discussion.

summary(fit_partpool)
## Linear mixed model fit by REML ['lmerMod']
## Formula: log_radon ~ (1 | county)
##    Data: radon
## 
## REML criterion at convergence: 2184.9
## 
## Scaled residuals: 
##     Min      1Q  Median      3Q     Max 
## -4.6880 -0.5884  0.0323  0.6444  3.4186 
## 
## Random effects:
##  Groups   Name        Variance Std.Dev.
##  county   (Intercept) 0.08861  0.2977  
##  Residual             0.58686  0.7661  
## Number of obs: 919, groups:  county, 85
## 
## Fixed effects:
##             Estimate Std. Error t value
## (Intercept)    1.350      0.047   28.72
  • The random effects portion of the lmer output provides a point estimate of the variance of component \(\sigma^2_{\alpha} = 0.09\) and the model’s residual variance, \(\sigma_\epsilon = 0.57\).
  • The fixed effect here is interpreted in the same way that we would in a normal fixed effects mean model, as the global predicted value of the outcome of log_radon.
  • The random intercepts aren’t automatically shown in this output. We can visualize these using a forestplot. We use the plot_model() function from the sjPlot package, on the fit_partpool model, we want to see the random effects (type="re"), and we want to sort on the name of the random variable, here it’s "(Intercept)".
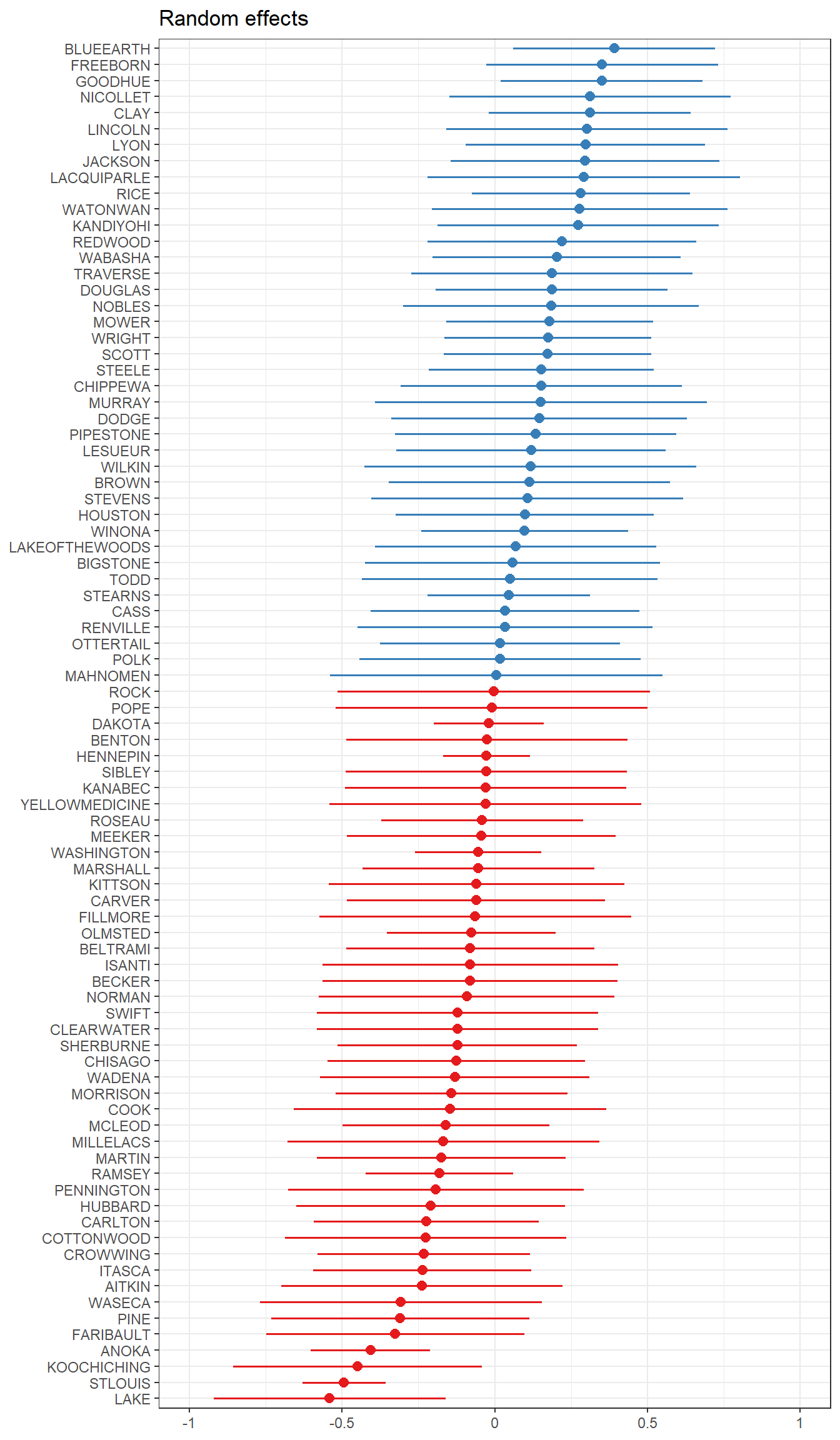
sjPlot::plot_model(fit_partpool, type="re", sort.est = "(Intercept)", y.offset = .4)

Notice that these effects are centered around 0. Refering back 17.2, the intercept \(\beta_{0j}\) was modeled equal to some average intercept across all groups \(\gamma_{00}\), plus some difference. What is plotted above is listed in a table below, showing that if you add that random effect to the fixed effect of the intercept, you get the value of the random intercept for each county.

showri <- data.frame(Random_Effect   = unlist(ranef(fit_partpool)), 
                     Fixed_Intercept = fixef(fit_partpool), 
                     RandomIntercept = unlist(ranef(fit_partpool))+fixef(fit_partpool))
                
rownames(showri) <- rownames(coef(fit_partpool)$county)
kable(head(showri))
Random_Effect Fixed_Intercept RandomIntercept
AITKIN -0.2390574 1.34983 1.1107728
ANOKA -0.4071256 1.34983 0.9427047
BECKER -0.0809977 1.34983 1.2688325
BELTRAMI -0.0804277 1.34983 1.2694025
BENTON -0.0254506 1.34983 1.3243796
BIGSTONE 0.0582831 1.34983 1.4081133

17.4.1 Comparison of estimates

  • By allowing individuals within counties to be correlated, and at the same time let counties be correlated, we allow for some information to be shared across counties.
  • Thus we come back to that idea of shrinkage. Below is a numeric table version of the plot in Section ??.
cmpr.est <- data.frame(Mean_Model       = coef(fit_completepool), 
                       Random_Intercept = unlist(ranef(fit_partpool))+fixef(fit_partpool), 
                       Fixed_Effects    = coef(fit_nopool))
rownames(cmpr.est) <- rownames(coef(fit_partpool)$county)
kable(head(cmpr.est))
Mean_Model Random_Intercept Fixed_Effects
AITKIN 1.264779 1.1107728 0.7149352
ANOKA 1.264779 0.9427047 0.8908486
BECKER 1.264779 1.2688325 1.0900084
BELTRAMI 1.264779 1.2694025 1.1933029
BENTON 1.264779 1.3243796 1.2822379
BIGSTONE 1.264779 1.4081133 1.5367889