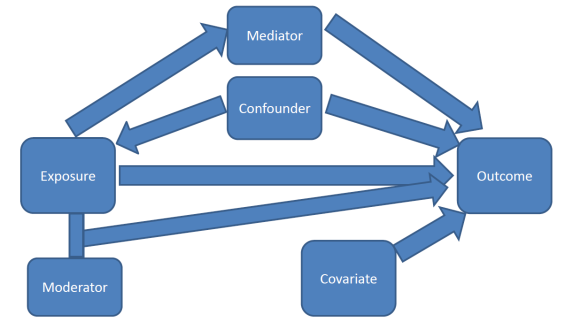
9.6 Confounding

One primary purpose of a multivariable model is to assess the relationship between a particular explanatory variable \(x\) and your response variable \(y\), after controlling for other factors.

All the ways covariates can affect response variables
All the ways covariates can affect response variables

Credit: A blog about statistical musings

Easy to read short article from a Gastroenterology journal on how to control confounding effects by statistical analysis. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4017459/

Other factors (characteristics/variables) could also be explaining part of the variability seen in \(y\).

If the relationship between \(x_{1}\) and \(y\) is bivariately significant, but then no longer significant once \(x_{2}\) has been added to the model, then \(x_{2}\) is said to explain, or confound, the relationship between \(x_{1}\) and \(y\).

Steps to determine if a variable \(x_{2}\) is a confounder.

  1. Fit a regression model on \(y \sim x_{1}\).
  2. If \(x_{1}\) is not significantly associated with \(y\), STOP. Re-read the “IF” part of the definition of a confounder.
  3. Fit a regression model on \(y \sim x_{1} + x_{2}\).
  4. Look at the p-value for \(x_{1}\). One of two things will have happened.
    • If \(x_{1}\) is still significant, then \(x_{2}\) does NOT confound (or explain) the relationship between \(y\) and \(x_{1}\).
    • If \(x_{1}\) is NO LONGER significantly associated with \(y\), then \(x_{2}\) IS a confounder.

This means that the third variable is explaining the relationship between the explanatory variable and the response variable.

Note that this is a two way relationship. The order of \(x_{1}\) and \(x_{2}\) is invaraiant. If you were to add \(x_{2}\) to the model before \(x_{1}\) you may see the same thing occur. That is - both variables are explaining the same portion of the variance in \(y\).